X.芝诺悖论
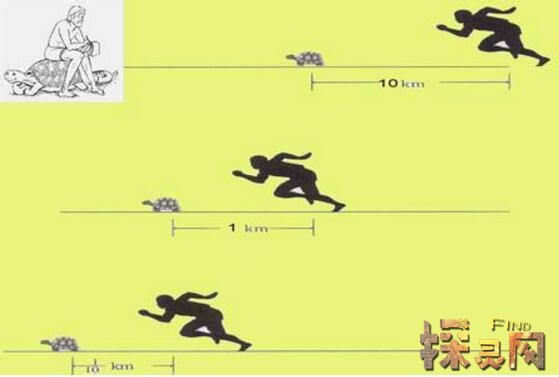
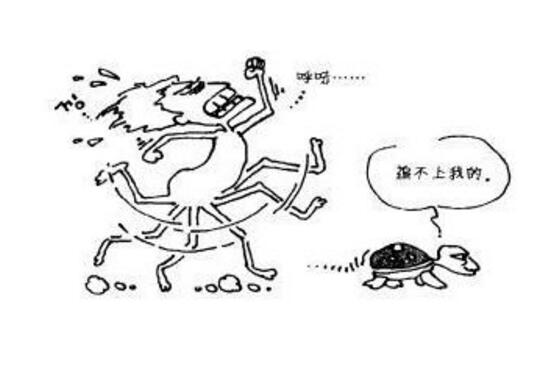
芝诺悖论是古希腊哲学家芝诺提出的一组悖论。在亚里士多德的书《物理学》中也可以找到其中的几个悖论。在跑步比赛中,如果最慢的乌龟在一开始领先最快的希腊战士阿喀琉斯,那么乌龟永远也追不上阿喀琉斯.可以说,为了追上乌龟,战士必须先到达乌龟当前的位置;当阿喀琉斯到达这个位置时,乌龟已经前进了很长一段路。当战士第二次前进到乌龟所在的位置时,乌龟又继续前进.所以,从某种意义上说,阿喀琉斯永远也追不上乌龟.[查看详细信息]
XI。巴伯悖论
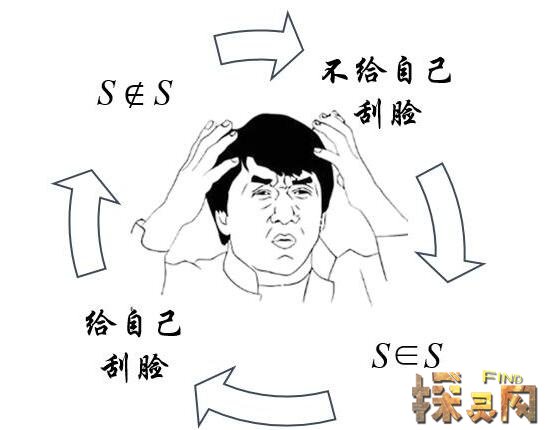
这个悖论是著名数学家罗素提出的罗斯悖论的延伸。这个理发师的例子闻名于世,甚至引发了第三次数学危机!理发师悖论被一个广告延伸。有一个很有趣的故事!一个理发师打出广告,“我要给这个城市里所有自己不刮胡子的人刮胡子,我只给这些人刮。”但是有一天,理发师在镜子里看到自己的胡子长了,那么他可以自己刮胡子吗.[查看详细信息]
十二。电梯悖论

电梯悖论是世界十大著名悖论之一,应用于生活的最多。人们在乘坐电梯的时候,往往会被一个奇怪的概率所迷惑,这就是电梯悖论。明知道电梯独立运行与任何人无关,每层花费的时间是相等的,但是无论是顶层的王小姐还是底层的李小姐都很苦恼。李小姐觉得,每当她想上楼的时候,电梯总是在那个时间下楼,而王小姐则相反.[查看详细信息]
十三。色盲

如果有一个人,他有一种奇怪的色盲。他看到的两种颜色和别人不一样。他会把蓝色当成绿色,绿色当成蓝色。但是,他不知道自己和别人不一样。别人看到的是蓝天,他看到的是绿色,他却和别人一样被称为“蓝色”。草是绿的,但他看到的是蓝的,他却把蓝叫做“绿”。所以他和别人都不知道他和别人的区别。怎么才能让他知道自己是色盲?如果你是色盲呢?如何证明自己不是上面问题中的主人公?