芝诺悖论是古希腊哲学家芝诺提出的一组悖论。在亚里士多德的书《物理学》中也可以找到其中的几个悖论。根据乌龟悖论,在跑步比赛中,如果最慢的乌龟在一开始领先最快的希腊战士阿喀琉斯,那么乌龟永远不会被阿喀琉斯超过.是不是很不可思议?
芝诺悖论——永远追不上的乌龟。
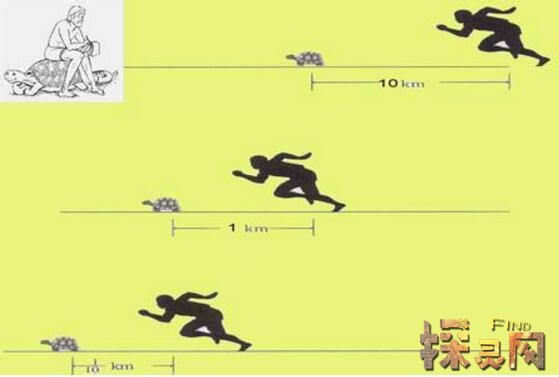
阿喀琉斯和乌龟之间的悖论是一个神奇的解释。在跑步比赛中,如果最慢的乌龟在开始时领先最快的希腊战士阿喀琉斯,那乌龟永远也追不上阿喀琉斯.可以说,战士要想追上乌龟,必须先到达乌龟现在的位置;当阿喀琉斯到达这个位置时,乌龟已经前进了很长一段路。当战士第二次前进到乌龟所在的位置时,乌龟又继续前进.所以,从某种意义上来说,阿喀琉斯永远也追不上乌龟!
芝诺悖论的创始人亚里士多德认为,当追赶者和被追赶者之间的距离越来越小时,追赶所需的时间也越来越短。他说无穷多个越来越小的数之和是有限的,所以可以在有限的时间内追上.虽然我们可以从数学上计算出阿喀琉斯在何时何地追上了乌龟,但一些哲学家认为这些证明仍然没有解决悖论提出的问题。

他们的论点是,乌龟爬到一个点的时候,只要你不同时到达这个点,你到达乌龟的地方就不是乌龟到达的点。这是因为时间不同!你马上到的乌龟说的不是乌龟到那个点的时间。虽然这在空间上是同一个地方,但在时间上永远不会是同一个地方,所以你永远也追不上它。
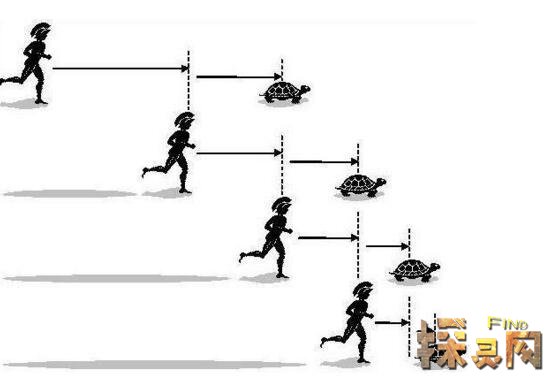
一个人从A点走到B点,要先走完一半的路程,再走完剩下的一半路程,以此类推,再走完剩下的一半路程,另一半可以分开.“这就像是一个循环继续下去,因为总有一半可以被分解,所以一个人会永远。当A和B无限接近时,也就是说人不能动,只能静止不动!

这么说吧,当追赶者和被追赶者的距离越来越小时,追赶所需的时间也越来越小。他说无限多个越来越小的数之和是有限的,所以可以在有限的时间内追上。但他的解释并不严格,因为我们很容易举出一个反例:调和级数1 1/2 1/3 1/4 ……的每一项都减小,但其和发散。
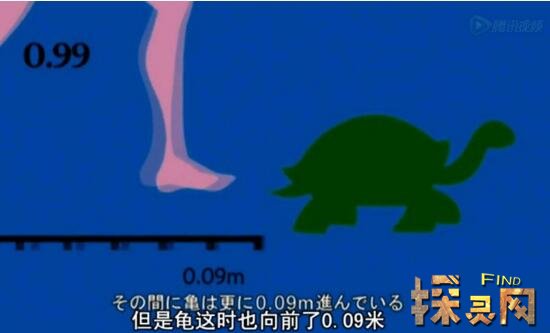
虽然我们可以用数学方法来计算阿喀琉斯在何时何地追上了乌龟,但一些哲学家认为这些证明仍然没有解决悖论提出的问题。令人惊讶的是,芝诺悖论在作家中非常流行。列夫托尔斯泰在《战争与和平》讲过阿喀琉斯和乌龟的故事!







